RSA gilt als das erste asymmetrische Verschlüsselungsverfahren. Es wurde von Ronald Rivest, Adi Shamir und Leonard Adleman entwickelt. Alle drei arbeiteten damals im MIT-Labor für Computerwissenschaften und wurden durch einen Artikel von Withfield Diffie und Martin Hellman auf das Problem der asymmetrischen Verschlüsselung aufmerksam gemacht. Im Prinzip geht es dabei darum eine Funktion zu finden, die nur in eine Richtung berechnet werden kann. Bei so einer Funktion ist es einfach aus einer gegebenen Zahl ein Ergebnis zu berechnen. Aus dem Ergebnis wieder die anfängliche Zahl zu berechnen ist dagegen nur mit erheblichem Aufwand möglich.
Die Lösung für das Problem sind Primzahlen. Primzahlen sind Zahlen, die nur durch 1 oder sich selber Teilbar sind. Beispielsweise sind 7 oder 19 Primzahlen. Es ist einfach das Produkt aus 7 und 19 zu berechnen. Aus 133 allerdings wieder beide Primzahlen zu erhalten ist bedeutend schwerer. Hierfür muss man von Anfang an alle Primzahlen durchprobieren. Mann beginnt also mit 2, 3,… und teilt die 133 so lange bis eine Zahl ohne Rest heraus kommt. Eine Zahl die das Produkt aus 2 Primzahlen ist kann NUR durch diese beiden Zahlen geteilt werden. Das ist das schöne an Primzahlen. Es gibt kein anderes Produkt aus zwei Zahlen die 133 ergeben als das Produkt von 7 und 19.
Für den weiteren Teil bezeichnen wir die beiden Primzahlen mit ![]() und
und ![]() . Das Produkt beider Zahlen als
. Das Produkt beider Zahlen als ![]() .
.
(1) ![]()
Wie findet man nun Primzahlen? Eine Primzahl ist ja, wie bereits erwähnt, durch keine andere Zahl als sich selber zu teilen. Eine Möglichkeit Primzahlen zu finden ist es daher alle bekannten Primzahlen ![]() miteinander zu Multiplizieren. Das Ergebnis daraus addiert man mit 1. Der dadurch entstandene Wert ist eine neue Primzahl
miteinander zu Multiplizieren. Das Ergebnis daraus addiert man mit 1. Der dadurch entstandene Wert ist eine neue Primzahl ![]() .
.
(2) ![]()
Nehmen wir also an wir kennen alle Primzahlen bis 7. Das sind 2, 3, 5 und 7. Das Produkt aller Zahlen + 1 ist demnach:
![]()
Tatsächlich ist 211 eine Primzahl. Es gibt jedoch noch jede Menge Primzahlen die zwischen 7 und 211 liegen. Um mit dieser Methode jedoch weiter machen zu können brauchen wir bekanntlich alle Zahlen bis 211. Das ganze ist also nicht sehr effektiv. Letztendlich bleibt uns nichts weiteres übrig als alle Zahlen selber durchzuprobieren. Genau aus diesem Grund sind Primzahlen in der Kryptographie auch so beliebt.
Als Übung kann man einmal selbst ausprobieren alle Primzahlen von 0-100 zu finden. Am besten werden hierfür alle Zahlen auf ein Blatt Papier geschrieben. Wenn man nun eine Primzahl gefunden hat kann man diese markieren. Es können zudem alle vielfachen der Primzahl durchgestrichen werden, da diese ja durch die Primzahl teilbar sind und daher keine Primzahlen mehr seien können. Beispielsweise ist 3 eine Primzahl. 6, 9, 12, … können demnach keine Primzahlen mehr sein. Die nächste nicht markierte Zahl ist dann die nächste Primzahl.
Alle Primzahlen bis 100 lauten: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Ein beliebtes Werkzeug der Kryptographie ist der Modulo. Der Modulo ist der Rest einer Division. Beispielsweise ist der Modulo von 5 und 3 = 2, da 5/3 = 1 Rest 2. Der Modulo ![]() aus
aus ![]() und
und ![]() kann als
kann als ![]() geschrieben werden.
geschrieben werden.
(3) 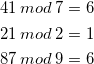
Als nächstes muss der Begriff der Kongruenz geklärt werden. Die Kongruenz ist eine Beziehung zwischen drei Zahlen. Man nennt zwei Zahlen kongruent bezüglich der dritten zahl, wenn diese bei einer Division durch die dritte Zahl (den Modul) den gleichen Rest haben. Beispielsweise sind 5 und 11 kongruent bezüglich 3, da 5/3 = 1 Rest 2 und 11/3 = 3 Rest 2. Beide Zahlen haben den gleichen Rest. Um die Kongruenz zwischen a und b bezüglich n darzustellen schreibt man ![]()
(4) ![]()
Um diesen Sachverhalt bei zwei Zahlen schnell feststellen zu können berechnet man zuerst ![]() . Das Ergebnis muss sich nun ohne Rest durch
. Das Ergebnis muss sich nun ohne Rest durch ![]() Teilen lassen.
Teilen lassen. ![]() und
und ![]() sind also kongruent, wenn
sind also kongruent, wenn
(5) ![]()
Das letzte Konzept das wir brauchen ist der größte gemeinsame Teiler, kurz ![]() . Der
. Der ![]() beschreibt, wie der Name schon sagt, die größte natürliche Zahl, durch die zwei verschiedene Zahlen geteilt werden können, ohne das ein Rest entsteht. Die 12 kann beispielsweise durch 1, 2, 3, 4, 6 und 12 geteilt werden. Die 18 kann ducht 1, 2, 3, 6, 9 und 18 geteilt werden. Der größter gemeinsame Teiler von 12 und 18 ist 6.
beschreibt, wie der Name schon sagt, die größte natürliche Zahl, durch die zwei verschiedene Zahlen geteilt werden können, ohne das ein Rest entsteht. Die 12 kann beispielsweise durch 1, 2, 3, 4, 6 und 12 geteilt werden. Die 18 kann ducht 1, 2, 3, 6, 9 und 18 geteilt werden. Der größter gemeinsame Teiler von 12 und 18 ist 6.
(6) ![]()
Es gilt zudem:
(7) ![]()
Nun geht es ans Eingemachte. Wie bereits erwähnt funktioniert RSA mit zwei Schlüsseln. Einem privaten und einem öffentlichen. Mit beiden Schlüsseln können Nachrichten verschlüsselt werden. Entschlüsseln kann man die Nachrichten jedoch nur mit dem Gegenstück.
Angenommen jemand möchte uns eine verschlüsselte Nachricht ![]() schicken, dann nimmt er den öffentlichen Schlüssel
schicken, dann nimmt er den öffentlichen Schlüssel ![]() und verschlüsselt damit die Nachricht
und verschlüsselt damit die Nachricht ![]() . Der öffentliche Schlüssel ist dabei für jeden verfügbar. Um die Nachricht wieder zu entschlüsseln benutzen wir nun unseren privaten Schlüssel
. Der öffentliche Schlüssel ist dabei für jeden verfügbar. Um die Nachricht wieder zu entschlüsseln benutzen wir nun unseren privaten Schlüssel ![]() und wenden ihn auf die verschlüsselte Nachricht
und wenden ihn auf die verschlüsselte Nachricht ![]() an und erhalten dadurch wieder unsere Nachricht.
an und erhalten dadurch wieder unsere Nachricht.
(8) ![]()
Das ganze funktioniert auch in die andere Richtung. Beispielsweise möchte nun jemand von uns Wissen, ob wir wirklich derjenige sind, der wir vorgeben zu sein. In diesem Fall gibt er uns eine Nachricht die wir mit unserem privaten Schlüssel verschlüsseln sollen. Da nur wir den privaten Schlüssel haben kann das niemand anderes sonst tun. Entschlüsselt wird die Nachricht in diesem Fall mit dem öffentlichen Schlüssel. Die von uns verschlüsselte Nachricht kann von jedem entschlüsselt werden, da der öffentliche Schlüssel für jeden zugänglich ist. Es geht dabei also nicht darum eine Nachricht zu entschlüsseln, sondern vielmehr darum zu beweisen, dass man selbst im Besitz des privaten Schlüssels ist.
Um einen privaten und öffentlichen Schlüssel zu generieren sind 5 einfache Schritte notwendig.
- Finde zwei Primzahlen
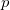 und
und 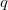
- Berechne das Produkt
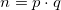
- Berechne
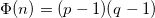
- Finde eine Zahl
 welche Teilerfremd zu
welche Teilerfremd zu 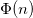 ist. Es gilt also
ist. Es gilt also 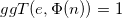
- Finde eine Zahl
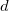 für die gilt, dass
für die gilt, dass 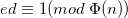
Das war es auch schon. Der private Schlüssel ist ![]() , während
, während ![]() und
und ![]() zusammen den öffentliche Schlüssel darstellen. Gerade die Schritte 4 und 5 sehen schwieriger zu berechnen aus als sie sind. Wir kommen später in einem Beispiel darauf zurück. Die beiden Primzahlen
zusammen den öffentliche Schlüssel darstellen. Gerade die Schritte 4 und 5 sehen schwieriger zu berechnen aus als sie sind. Wir kommen später in einem Beispiel darauf zurück. Die beiden Primzahlen ![]() und
und ![]() können nun ohne Bedenken verworfen werden. Zum ver- und entschlüsseln der Nachricht werden diese nicht mehr gebraucht, sie sind jedoch ein großes Sicherheitsrisiko wenn sie bekannt werden.
können nun ohne Bedenken verworfen werden. Zum ver- und entschlüsseln der Nachricht werden diese nicht mehr gebraucht, sie sind jedoch ein großes Sicherheitsrisiko wenn sie bekannt werden.
Um einen Buchstaben ![]() der Nachricht
der Nachricht ![]() mit dem öffentlichen Schlüssel
mit dem öffentlichen Schlüssel ![]() und
und ![]() zu verschlüsseln wird folgende Formel benutzt:
zu verschlüsseln wird folgende Formel benutzt:
(9) ![]()
Dabei ist ![]() das verschlüsselte Ergebnis and Position
das verschlüsselte Ergebnis and Position ![]() . Um das ganze nun wieder in den ursprünglichen Buchstaben
. Um das ganze nun wieder in den ursprünglichen Buchstaben ![]() zu entschlüsseln benötigen wir den privaten Schlüssel
zu entschlüsseln benötigen wir den privaten Schlüssel ![]() und den Modul
und den Modul ![]() .
.
(10) ![]()
Am besten machen wir das ganze einmal mit einem Beispiel. Zuerst brauchen wir also zwei Primzahlen. In unserem Beispiel nehmen wir 5 und 13. Aus beiden Zahlen bilden wir den Modul ![]() .
.
(11) ![]()
Jetzt müssen wir ![]() berechnen. Hierführ setzen wir unsere Zahlen in die Formel ein.
berechnen. Hierführ setzen wir unsere Zahlen in die Formel ein.
(12) 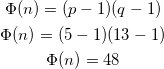
Jetzt muss der Exponent ![]() gefunden werden. Dieser muss Teilerfremd zu
gefunden werden. Dieser muss Teilerfremd zu ![]() sein. Wir benötigen also eine Zahl, durch welche sich 48 nicht ohne Rest teilen lässt. Ist die gesuchte Zahl gerade, so kann eine ungerade Zahl verwendet werden und umgekehrt. Wir benutzen in diesem Beispiel die Zahl 5. Damit haben wir schon einmal alles was wir brauchen um eine Nachricht zu verschlüsseln. Wir möchten jetzt die Nachricht „HALLO WELT“ verschlüsseln. Hiefür wandeln wir die Buchstaben in Zahlen um. Das geschieht am besten nach dem ABC. Also ist A=1, B=2,… Das Leerzeichen ist in diesem Fall 28.
sein. Wir benötigen also eine Zahl, durch welche sich 48 nicht ohne Rest teilen lässt. Ist die gesuchte Zahl gerade, so kann eine ungerade Zahl verwendet werden und umgekehrt. Wir benutzen in diesem Beispiel die Zahl 5. Damit haben wir schon einmal alles was wir brauchen um eine Nachricht zu verschlüsseln. Wir möchten jetzt die Nachricht „HALLO WELT“ verschlüsseln. Hiefür wandeln wir die Buchstaben in Zahlen um. Das geschieht am besten nach dem ABC. Also ist A=1, B=2,… Das Leerzeichen ist in diesem Fall 28.
H = 08
A = 01
L = 12
L = 12
O = 15
_ = 28
W = 23
E = 05
L = 12
T = 20
Die Nachricht 08 01 12 12 15 28 23 05 12 20 kann Anschließend mit dem Exponenten ![]() = 5 und dem Modul
= 5 und dem Modul ![]() = 65 verschlüsselt werden.
= 65 verschlüsselt werden.
(13) ![]()
(14) 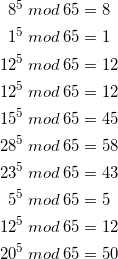
Unsere verschlüsselte Nachricht lautet nun 08 01 12 12 45 58 43 05 12 50. Ich habe hiefür einen Taschenrechner benutzt. Es gibt aber auch einen Trick um den Modul auf dem Papier zu berechnen.
(15) ![]()
Zudem gilt.
(16) ![]()
und
(17) ![]()
Diese Rechenregel kann man auch auf unsere Rechnung übertragen. Das ganze einmal an einem Beispiel verdeutlicht.
(18) 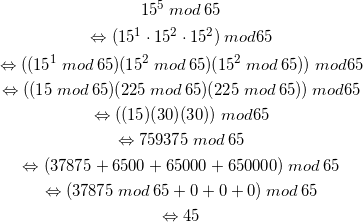
Jedem, der schon einmal etwas mit Kryptographie zu tun hatte sollte hierbei sofort etwas auffallen: Falls wir wirklich so verschlüsseln wollen wäre das schlecht. Der gleiche Buchstabe erhält immer die gleiche verschlüsselte Zahl. Anhand der Häufigkeitsanalyse könnte auf diese Art sehr schnell die Nachricht entschlüsselt werden. In diesem Beispiel ist es sogar so, dass nur drei Buchstaben durch die Verschlüsselung überhaupt geändert haben. Man kann hier kaum von einer vernünftigen Verschlüsselung sprechen. Aus diesem Grund werden mehrere Buchstaben zu einem Block zusammengefasst. Beispielsweise wird aus 02 und 05, 0205 gemacht. Dieser gesamte Block wird anschließend verschlüsselt. Ist für den letzten Buchstaben kein zweiter Buchstabe vorhanden, so wird der Rest mit 00 aufgefüllt. Zudem sollte der Modul ![]() möglichst groß sein. Um dieses Beispiel jedoch einfach zu halten habe ich den Modul möglichst klein gehalten. Der Modul muss jedoch immer größer sein, als der zu verschlüsselnde Block. Wäre dies nicht der Fall, könnte keine Eindeutigkeit mehr bei der Entschlüsselung hergestellt werden.
möglichst groß sein. Um dieses Beispiel jedoch einfach zu halten habe ich den Modul möglichst klein gehalten. Der Modul muss jedoch immer größer sein, als der zu verschlüsselnde Block. Wäre dies nicht der Fall, könnte keine Eindeutigkeit mehr bei der Entschlüsselung hergestellt werden.
Das ganze können wir nun mit dem privaten Schlüssel ![]() wieder entschlüsseln. Diesen müssen wir zunächst jedoch Berechnen. Um den privaten Schlüssel zu erhalten benötigen wir eine Zahl
wieder entschlüsseln. Diesen müssen wir zunächst jedoch Berechnen. Um den privaten Schlüssel zu erhalten benötigen wir eine Zahl ![]() für die gilt, dass
für die gilt, dass
(19) ![]()
Wenn wir unsere Zahlen einsetzen erhalten wir: ![]() . Das heist also, dass
. Das heist also, dass ![]() ein vielfaches von 48 sein muss. Das ganze lässt sich auf verschiedene Arten durchprobieren. Ich stelle hierfür die Formel um und sage:
ein vielfaches von 48 sein muss. Das ganze lässt sich auf verschiedene Arten durchprobieren. Ich stelle hierfür die Formel um und sage: ![]() . Die Zahl
. Die Zahl ![]() ist dabei beliebig und muss immer weiter erhöht werden, bis man eine Zahl gefunden hat, die sich durch 5 Teilen lässt. In unserem Fall ist
ist dabei beliebig und muss immer weiter erhöht werden, bis man eine Zahl gefunden hat, die sich durch 5 Teilen lässt. In unserem Fall ist ![]() . Dann ist
. Dann ist ![]() und damit ist
und damit ist ![]() . Mehr brauchen wir nicht um die Nachricht wieder zu entschlüsseln. Um in etwa die Möglichen Zahlen einschätzen zu können muss man nur
. Mehr brauchen wir nicht um die Nachricht wieder zu entschlüsseln. Um in etwa die Möglichen Zahlen einschätzen zu können muss man nur ![]() durch
durch ![]() Teilen. In unserem Beispiel erhält man für
Teilen. In unserem Beispiel erhält man für ![]() die Zahlen 9.6, 19.2, 28,2 und 38,4. Mit 28,2 lagen wir dabei schon sehr nahe an der 29.
die Zahlen 9.6, 19.2, 28,2 und 38,4. Mit 28,2 lagen wir dabei schon sehr nahe an der 29.
(20) ![]()
Die Nachricht können wir nun ganz einfach Entschlüsseln.
(21) 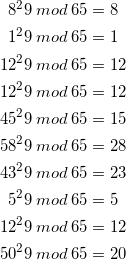
Was brauchen wir nun, wenn wir den privaten Schlüssel ![]() nicht haben und trotzdem die Nachricht entschlüsseln wollen? Um
nicht haben und trotzdem die Nachricht entschlüsseln wollen? Um ![]() zu berechnen benötigen wir die beiden Primzahlen
zu berechnen benötigen wir die beiden Primzahlen ![]() und
und ![]() . Diese sollten jedoch streng geheim sein. Es bleibt uns also nichts anderes übrig als diese selbst zu berechnen. Beide Zahlen sind in dem Modul
. Diese sollten jedoch streng geheim sein. Es bleibt uns also nichts anderes übrig als diese selbst zu berechnen. Beide Zahlen sind in dem Modul ![]() enthalten. Aus diesem Grund sollte der Modul auch möglichst groß gewählt werden.
enthalten. Aus diesem Grund sollte der Modul auch möglichst groß gewählt werden.
Die Folgende Nachricht ist mit dem öffentlichen Schlüssel ![]() und
und ![]() verschlüsselt worden. Den privaten Schlüssel daraus zu berechnen und die Nachricht zu entschlüsseln überlasse ich dem Leser.
verschlüsselt worden. Den privaten Schlüssel daraus zu berechnen und die Nachricht zu entschlüsseln überlasse ich dem Leser.
2469 0599 0697 0548 2107 1928