Sortierverfahren: Mergesort

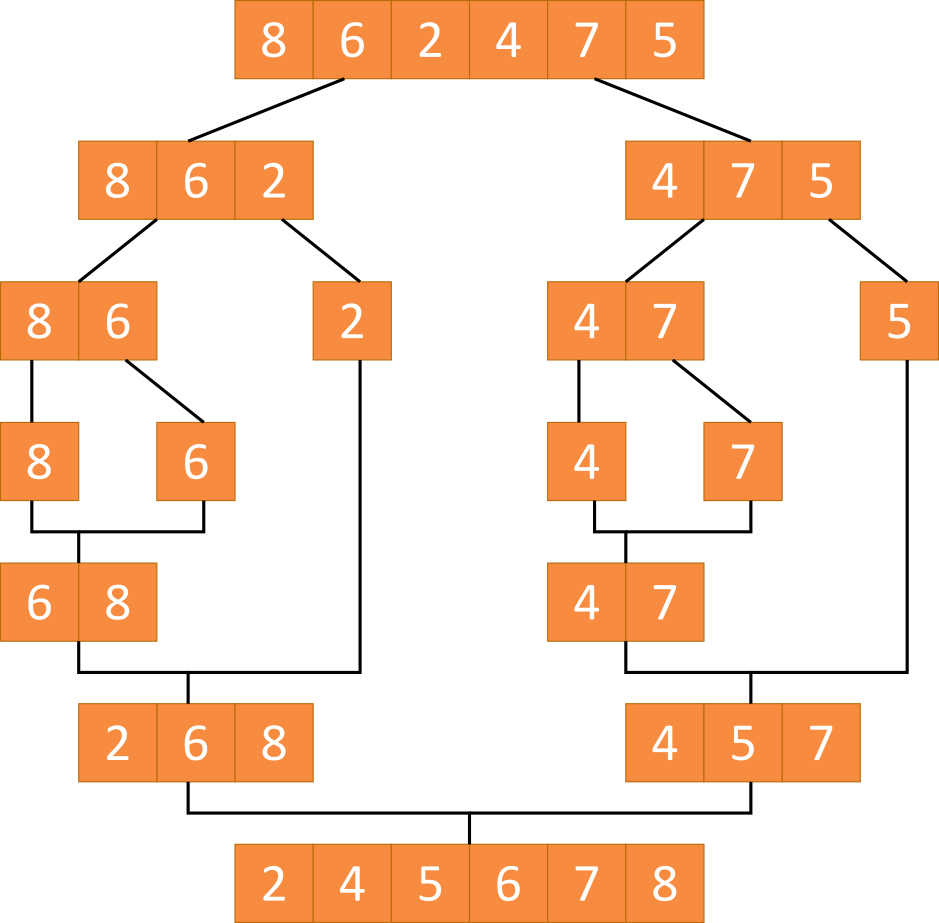
Mergesort ist ein stabiles Sortierverfahren, welches nach dem Teile-und-herrsche-Verfahren (divide and conquer) arbeitet.
Ein zu sortierendes Feld wird dabei in zwei gleich große Felder geteilt. Beide Felder werden im Anschluss wieder rekursiv in den Algorithmus gesteckt. Dies geschieht so lange, bis alle Felder in ihre einzelnen Elemente zerteilt wurden. Beide Elemente werden nun sortiert in ein neues Feld geschreiben. Diese Operation stellt nun kein Problem dar, da nur ein einizger Vergleich nötig ist um zu erkennen werlches Element zuerst in das Feld geschrieben wird. Dieses sortierte Feld wird dann an die aufrufende methode zurück gegeben. Die Aufrufende Methode hat nun zwei unabhängig sortierte Felder und muss diese nun ebenfalls sortieren und an deren aufrufende Methode zurück geben. Das sortieren von zwei bereits sortierten listen kann dadurch realisiert werden, indem jeweils nur die ersten Elemente betrachtet werden und das kleinste beider Elemente in die neue Liste eingefügt wird. Dies geschieht so lange, bis beide Teilfelder leer sind und alle Elemente in dem neuen Feld stehen. Sobald in die urpsüngliche Methode beendet ist sind alle Elemente in der Liste sortiert.

public class MergeSort {

	static <T extends Comparable<T>> T[] sort(T[] source) {
		if (source.length <= 1) {
			return source;
		}
		T[] left = ArrayTools.copy(source, 0, source.length/2 - 1);
		T[] right = ArrayTools.copy(source, source.length/2, source.length - 1);
		return merge(sort(right), sort(left));
	}
	
	@SuppressWarnings("unchecked")
	static <T extends Comparable<T>> T[] merge(T[] left, T[] right) {
		T[] result = (T[]) Array.newInstance(left[0].getClass(), left.length + right.length);
		int posLeft = 0, arrayPos = 0, posRight = 0;
		while (arrayPos < result.length) {
			if (posLeft < left.length && (posRight >= right.length ||
					left[posLeft].compareTo(right[posRight]) <= 0)) {
				result[arrayPos] = left[posLeft];
				posLeft++;
			}
			else {
				result[arrayPos] = right[posRight];
				posRight++;
			}
			arrayPos++;
		}
		
		return result;
	}
}

Durch die enorme Anzahl an Rekursionen ist Mergesort in der hier gezeigten Form nicht sehr performant für große Listen. Die Rekursion sollte daher durch eine Schleife und einen Stack zum halten der Elemente ersetzt werden.

	static <T extends Comparable<T>> T[] iterativeSort(T[] source) {
		final Stack<T[]> divideStack = new LinkedStack<>();
		final Stack<T[]> mergeStack = new LinkedStack<>();
		divideStack.push(source);
		
		do {
			T[] item = divideStack.pop();
			if (item.length <= 1) {
				T[] itemToMerge = item;
				while(mergeStack.size() > 0 && (itemToMerge.length - mergeStack.peak().length >= 0 || divideStack.size() <= 0)) {
					itemToMerge = merge(mergeStack.pop(), itemToMerge);
				}
				
				mergeStack.push(itemToMerge);
			}
			else {
				divideStack.push(ArrayTools.copy(item, 0, item.length/2 - 1));
				divideStack.push(ArrayTools.copy(item, item.length/2, item.length - 1));
			}
		}
		while(divideStack.size() > 0);
		
		return (T[]) mergeStack.pop();
	}

Komplexität