Automatisches Differenzieren

Durch das automatische Differenzieren (autoDiff) ist es Programmen möglich mathematische Funktionen abzuleiten. Je nach Anwendungsfall kann dabei vorwärts oder rückwärts differenziert werden. Ich erkläre anhand eines Beispiels beide Vorgehensweisen und gehe auf die Vor- und Nachteile ein.

(1) $\begin{gather*} z = x^2 + 2x + sin(y) \end{gather*}$

Die obige Formel soll durch einen Algorithmus differenziert werden. Für ein Computerprogramm ist dies nicht so einfach, wie es zunächst scheint. Alle Rechenoperationen müssen einzeln mit Hilfe von elementaren Operationen ausgeführt und in Zwischenschritten abgespeichert werden.

n1 = x * x
n2 = 2 * x
n3 = sin(y)
n4 = n1 + n2
n5 = n4 + n3

In dem gezeigten Beispiel werden 5 Zwischenschritte benötigt um die Formel zu berechnen. Der Benutzer kann daraufhin die Variablen $x$ und $y$ initialisieren und das Ergebnis berechnen lassen.

Vorwärts-Modus

Um die oben gezeigte Formel zu differenzieren werden ebenfalls elementare Rechenoperationen benötigt, damit ein Algorithmus damit umgehen kann. Um dies zu ermöglichen wird auf die Kettenregel zurück gegriffen.

(2) $\begin{gather*} \frac{\delta f}{\delta x} = \frac{\delta f}{\delta u} \cdot \frac{\delta u}{\delta x} \end{gather*}$

Die Kettenregel lässt uns die gesamte Formel in einzelnen Schritten differenzieren. Genau das ist von Vorteil für ein Algorithmus, der eine Funktion ebenfalls in einzelnen Rechenschritten ausführt.

Ein Algorithmus könnte die oben gezeigte Formel wahlweise nach $x$ oder $y$ differenzieren. Dies ist für zwei Variablen noch vertretbar. Sobald eine Formel jedoch aus Hunderten Variablen besteht nicht mehr performant. Um dieses Problem zu lösen wird eine neue Variable $t$ eingeführt und $x$ und $y$ als Funktionen dieser angesehen.

(3) $\begin{gather*} x = x(t) \\ y = y(t) \end{gather*}$

Die einzelnen Rechenoperationen lassen sich anschließend nach $t$ differenzieren.

(4) $\begin{gather*} \frac{\delta n_1}{\delta t} = 2 x(t) \frac{\delta x}{\delta t} \\ \frac{\delta n_2}{\delta t} = 2 \frac{\delta x}{\delta t} \\ \frac{\delta n_3}{\delta t} = - cos(y(t)) \frac{\delta y}{\delta t} \\ \frac{\delta n_4}{\delta t} = \frac{\delta n_1}{\delta t} + \frac{\delta n_2}{\delta t} \\ \frac{\delta n_5}{\delta t} = \frac{\delta n_4}{\delta t} + \frac{\delta n_3}{\delta t} \end{gather*}$

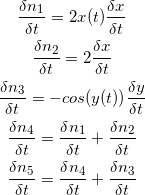
Das daraus resultierende Programm lässt sich wie folgt darstellen:

dn1 = 2 * x * dx
dn2 = 2 * dx
dn3 = -cos(y) * dy
dn4 = dn1 + dn2
dn5 = dn4 + dn3

Soll nun die partielle Ableitung nach $x$ berechnet werden, so muss $x(t)$ die identische Abbildung von $t$ sein und alle übrigen Funktionen müssen unabhängig von $t$ sein. Dadurch wird $x=t$ , $\delta x / \delta t = 1$ und
$\delta y / \delta t = 0$ . Als Beispiel möchten wir die Ableitung nach $x$ an der Stelle $x=3,y=2$ berechnen.

dn1 = 2 * 3 * 1
dn2 = 2 * 1
dn3 = -cos(2) * 0
dn4 = dn1 + dn2 //6 + 2
dn5 = dn4 + dn3 //8 + 0

Der Algorithmus kann die benötigten Variablen initialisieren und das gewünschte Ergebnis berechnen. Um die Ableitung für $y$ zu berechnen setzt man $\delta x / \delta t = 0$ und $\delta y / \delta t = 1$ .

Durch die Substitution mit $t$ muss nur einmal Differenziert werden. Der Wert der Ableitung kann für eine bestimmte Variable anschließend an jeder Stelle der Funktion berechnet werden. Muss eine Ableitung nach einer einzelnen Variable an vielen Stellen berechnet werden, so empfiehlt sich der Vorwärts-Modus. Man spart sich zwar das mehrmalige Differenzieren, ein großer Nachteil besteht jedoch darin, dass die Funktionswerte der Ableitung pro Variable berechnet werden müssen. Die Funktionswerte der partiellen Ableitungen nach $x$ und $y$ können nicht gleichzeitig berechnet werden.

Rückwärts-Modus

Der Rückwärts-Modus erlaubt es alle partiellen Ableitungen einer Funktion gleichzeitig zu berechnen. Dies ist jedoch nur an einer vorher definierten Funktionsstelle möglich. Für unser Beispiel entscheiden wir uns für die Werte $x=3$ und $y=\pi$ . Der Algorithmus arbeitet in zwei Schritten. Zuerst werden dabei die Funktionswerte für alle Rechenschritte berechnet. Im Zweiten Schritt wird mit Hilfe dieser die jeweilige Ableitung der Funkion ermittelt.

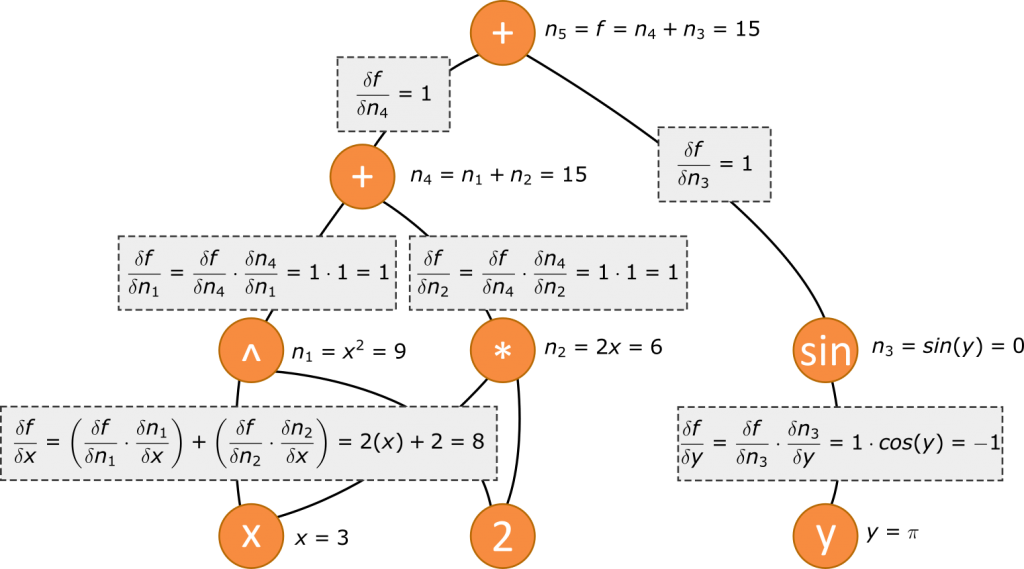
Die Funktionswerte zu berechnen ist für ein Computerprogramm nicht schwer. Die einzelnen Schritte werden zur Veranschaulichung nicht mehr als Rechenoperationen, sondern als Graph dargestellt.

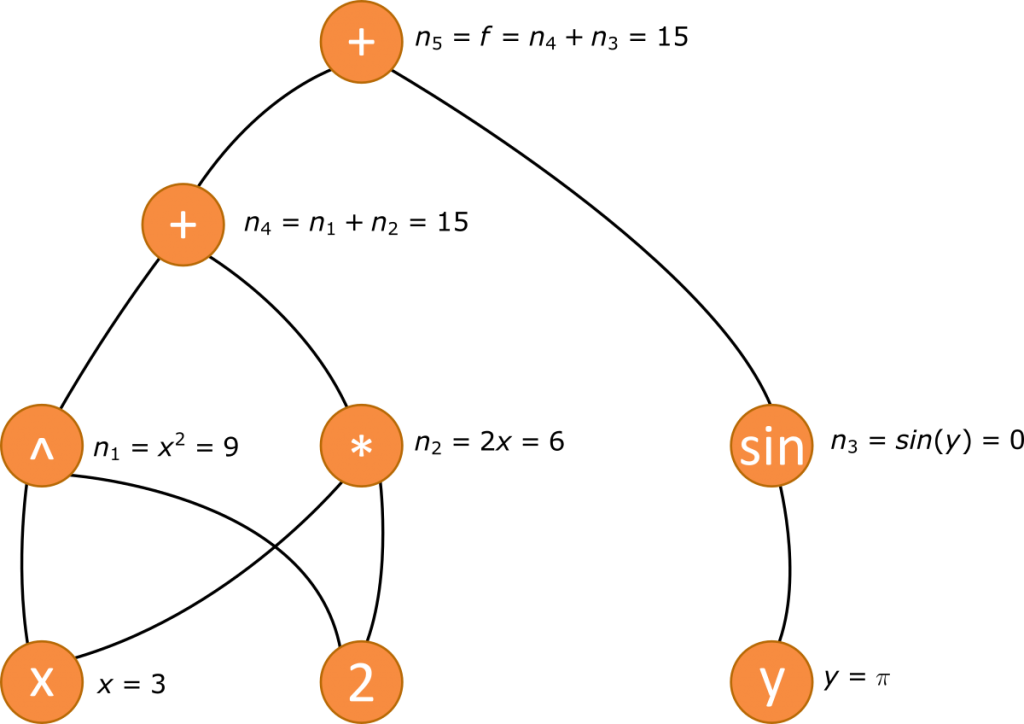
Berechnen der Funktionswerte: Der hier gezeigte Graph muss von unten nach oben betrachtet werden. Zuerst werden die Variablen initialisiert und anschließend die Funktionswerte berechnet.

Sobald alle Funktionswerte berechnet sind können die partiellen Ableitungen berechnet werden. Dies geschieht in umgekehrter Reihenfolge und für jeden Eingang in einen Knoten einzeln.

Der erste Knoten ist beispielsweise $n_5 = n_4 + n_3$ . Die Ableitungen können dabei sofort berechnet werden und müssen nicht mehr in Abhängigkeit einer Eingangsvariable stehen, da alle Funktionswerte bereits bekannt sind.

(5) $\begin{gather*} \frac{\delta n_5}{\delta n_4} = \frac{\delta }{\delta n_4} (n_4 + n_3) = \frac{\delta }{\delta n_4} (n_4 + 0) = 1 \end{gather*}$

Auch hierbei muss die Kettenregel angewandt werden. Für die Ableitung nach $n_1$ wird das Ergebnis aus $n_4$ benötigt.

(6) $\begin{gather*} \frac{\delta n_5}{\delta n_1} = \frac{\delta n_5}{\delta n_4} \cdot \frac{\delta n_4}{\delta n_1} \end{gather*}$

Das ganze ist ziemlich simpel und entspricht einfach nur einer absteigenden Abarbeitung im Graphen. Hat ein Knoten, wie beispielsweise $n_4$ , zwei Eingänge, so wird nach beiden Eingängen ( $n_1$ und $n_2$ ) separat die Ableitung gebildet. Besitzt ein Knoten zwei Ausgänge, so müssen beide Ableitungen addiert werden. Dies wird beispielsweise für $x$ gemacht.

Bei dem Rückwärts-Modus erhält man für alle Variablen die Funktionswerte der partiellen Ableitungen. Er eignet sich besonders für Aufgaben bei denen man an einer bestimmten Funktionsstelle alle partiellen Ableitungen benötigt. Ein Beispiel hierfür ist die Berechnung des Gradienten einer Fehlerfunktion, wie sie in neuronalen Netzen zum Einsatz kommt. Ohne auf Näherungen angewiesen zu sein kann durch automatische Differenzierung die Ableitung von Fehlern für hunderte Features gleichzeitig berechnet werden.