Ein binärer Heap ist eine Datenstruktur zum sortieren von Elementen. Es handelt sich dabei um einen Baum, dessen Knoten wahlweise absteigend oder aufsteigend angeordnet sind. Jeder Knoten selbst kann auf bis zu zwei weitere Knoten verweisen. Besitzen alle darunterliegenden Knoten einen kleineren Wert als der eigentliche Knoten, so erfüllt der Baum die Max-Heap-Bedingung. Sind die Kinder-Knoten absteigend sortiert, so erfüllt der Baum die Min-Heap-Bedingung.
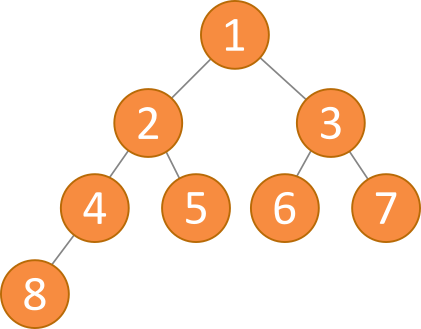
Bein einem binären Heap ![]() stehen die Kinder- und Eltern-Knoten in einer Relation zueinander. Die Kinder-Knoten selbst stehen jedoch in keiner Relation.
stehen die Kinder- und Eltern-Knoten in einer Relation zueinander. Die Kinder-Knoten selbst stehen jedoch in keiner Relation.
(1) ![]()
Ein binärer Heap ist immer balanciert. Die unterste Ebene wird dabei linksbündig aufgefüllt, wie auf der Abbildung zu sehen. Diese Eigenschaft erlaubt es den Heap effizient in einem Array zu speichern. Anhand des Indexes eines Knotens ![]() kann auf dessen Eltern- oder Kinder-Knoten zugegriffen werden. Zu beachten ist dabei, dass ein Array bei 0 beginnt.
kann auf dessen Eltern- oder Kinder-Knoten zugegriffen werden. Zu beachten ist dabei, dass ein Array bei 0 beginnt.
(2) 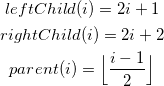

Einfügen
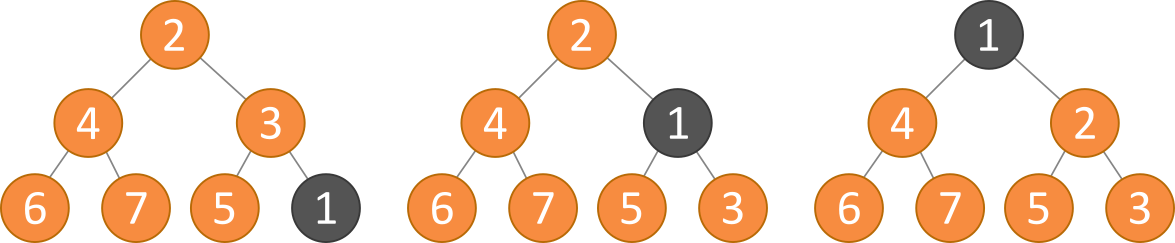
Um ein Element in den Heap einzusortieren wird dies an das Ende des Heap gesetzt. Im Anschluss wird rekursiv der zugehörige Eltern-Knoten betrachtet und sein Wert mit dem des eingefügten Knotens verglichen. Wird die Heap-Eigenschaft verletzt, so werden beide Knoten miteinander vertauscht. Dies geschieht so lange, bis die Heap-Eigenschaft wieder hergestellt wurde. Das rekursive austauschen der Knoten hin zum Root-Knoten wird als bubble-up bezeichnet.
Löschen
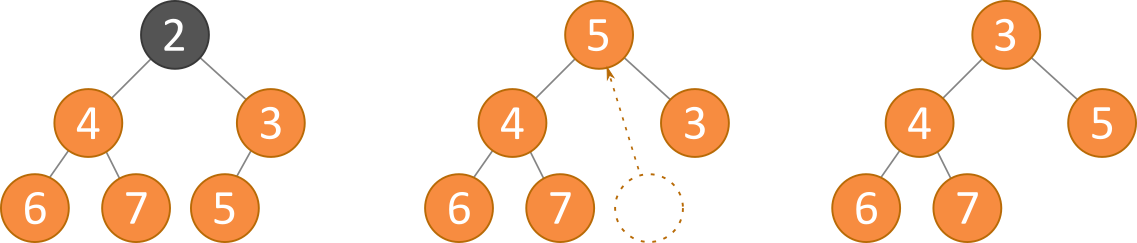
Um ein Element aus dem Heap zu löschen wird der zugehörige Knoten aus dem Heap entfernt. Anschließend wird der letzte Knoten des Heap genommen und an die Stelle des gelöschten Knotens gesetzt. Ausgehend von diesem Knoten wird die Heap-Eigenschaft hergestellt, indem er rekursiv mit seinen Kinderknoten ausgetauscht wird. Bei einem Min-Heap wird der größere, bei einem Max-Heap der kleinere der beiden Kinder-Knoten hergenommen. Dieser Vorgang wird bubble-down bezeichnet.
package com.florianbuchner.library.collection.tree;
import java.lang.IllegalArgumentException;
import com.florianbuchner.library.collection.list.ArrayList;
public class BinaryHeap<T extends Comparable<T>> {
private ArrayList<T> values;
private HeapType heapType;
public BinaryHeap(Class<T> classType, HeapType heapType) {
this.values = new ArrayList<>(classType);
this.heapType = heapType;
}
private int nextLeftIndex(int index) {
return index * 2 + 1;
}
private int nextRightIndex(int index) {
return index * 2 + 2;
}
private int previousIndex(int index) {
return (index - 1) / 2;
}
public void insert(T value) {
if (value == null) {
throw new IllegalArgumentException();
}
this.values.add(value);
this.bubbleUp(this.values.size() - 1);
}
public T remove() {
if (this.values.size() == 0) {
return null;
}
final T value = this.values.get(0);
this.values.replace(0, this.values.remove(this.values.size() - 1));
if (this.values.size() != 0) {
this.bubbleDown(0);
}
return value;
}
private void bubbleUp(int index) {
while(!this.validHeapAtIndex(index) && index > 0) {
final int previousIndex = this.previousIndex(index);
this.swapValue(index, previousIndex);
index = previousIndex;
}
}
private void bubbleDown(int index) {
int nextLeftIndex = this.nextLeftIndex(index);
while(!this.valideHeapAtIndex(index) && nextLeftIndex <= this.values.size() - 1) {
final int nextRightIndex = this.nextRightIndex(index);
final int nextChoosenIndex;
if (nextRightIndex > this.values.size() - 1) {
nextChoosenIndex = nextLeftIndex;
}
else if (this.heapType == HeapType.MAX_HEAP) {
nextChoosenIndex = (this.values.get(nextLeftIndex).compareTo(this.values.get(nextRightIndex)) >= 0 ) ?
nextLeftIndex : nextRightIndex;
}
else {
nextChoosenIndex = (this.values.get(nextLeftIndex).compareTo(this.values.get(nextRightIndex)) <= 0 ) ?
nextLeftIndex : nextRightIndex;
}
this.swapValue(index, nextChoosenIndex);
index = nextChoosenIndex;
nextLeftIndex = this.nextLeftIndex(index);
}
}
private boolean validHeapAtIndex(int index) {
final T value = this.values.get(index);
final int previousIndex = this.previousIndex(index);
final int nextLeftIndex = this.nextLeftIndex(index);
final int nextRightIndex = this.nextRightIndex(index);
if (this.heapType == HeapType.MAX_HEAP) {
return (previousIndex < 0 || value.compareTo(this.values.get(previousIndex)) <= 0) &&
(nextLeftIndex > this.values.size() - 1 || value.compareTo(this.values.get(nextLeftIndex)) >= 0) &&
(nextRightIndex > this.values.size() - 1 || value.compareTo(this.values.get(nextRightIndex)) >= 0);
}
else {
return (previousIndex < 0 || value.compareTo(this.values.get(previousIndex)) >= 0) &&
(nextLeftIndex > this.values.size() - 1 || value.compareTo(this.values.get(nextLeftIndex)) <= 0) &&
(nextRightIndex > this.values.size() - 1 || value.compareTo(this.values.get(nextRightIndex)) <= 0);
}
}
public void swapValue(int index1, int index2) {
T value = this.values.get(index1);
this.values.replace(index1, this.values.get(index2));
this.values.replace(index2, value);
}
public enum HeapType{
MAX_HEAP,
MIN_HEAP
}
}
Komplexität
| Operation | Durchschnitt | Worst case |
|---|---|---|
| Zugriff (root) | O(1) | O(1) |
| Suche | O(n) | O(n) |
| Einfügen | O(log n) | O(log n) |
| Löschen | O(log n) | O(log n) |