Sortierverfahren: Shellsort – Florian Buchner

Shellsort ist ein Sortierverfahren, welches auf Insertionsort basiert. Insertionsort bringt jedes Element an seine Position, indem das Element über den bereits sortierten Bereich iteriert und mit jedem darin enthaltenen Element verglichen wird. Shellsort funktioniert auf die gleiche Weise. Der Unterschied ist jedoch, dass Elemente, welche in einem bestimmten Abstand zueinander stehen, in mehreren Durchgängen vorsortiert werden.

Die zu sortierende Sequenz wird in Untersequenzen aufgeteilt. Eine Untersequenz ergibt sich aus allen Elementen, welche in einem bestimmten Abstand zueinander stehen. Bei der Sequenz 1,2,3,4,5,6,7 währe eine Untersequenz mit Abstand 2 beispielsweise 1,3,5,7 und 2,4,6. Diese Untersequenzen werden separat sortiert. Im Anschluss wird der Abstand für die Sequenz verringert und die Sortierung erneut ausgeführt. Dies geschieht so lange, bis der Abstand nur noch ein Element beträgt, was die Sortierung dann equivalent zu Insertionsort macht.

Bei Shellsort werden die Elemente in jedem Schritt etwas besser sortiert. Zuerst ist die Sortierung dabei sehr grob. Einzelne Elemente werden dabei jedoch mit nur wenigen Operationen um große Distanzen verschoben. Dadurch gelangen die einzelnen Elemente schneller in die Nähe ihrer Sollposition. Shellsort kann inplace ausgeführt werden ist jedoch kein stabiler Sortieralgorithmus.

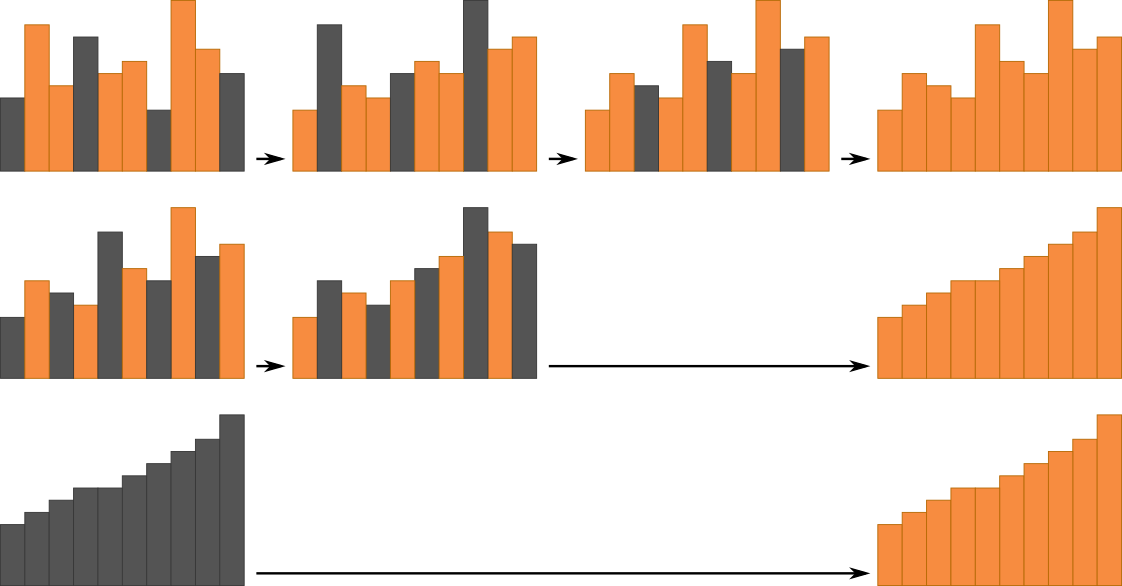
Shellsort mit einer Distanzfolge von 4,2,1. Es wird zuerst jedes vierte Element sortiert, ausgehend vom ersten Element. Dann ausgehend vom zweiten und dritten. Als nächstes wird jedes zweite Element, ausgehend vom ersten und zweiten sortiert. Zu guter letzt wird noch einmal jedes Element einzeln sortiert. Dieser Vorgang ist im allgemeinen sehr aufwendig. Da alle Elemente jedoch bereits sortiert waren ist in dem hier gezeigten Beispiel eine Sortierung nicht einmal mehr von Nöten.

Die einzelnen Abstände mit denen sortiert wird ist durch eine Distanzfolge bestimmt. Durch eine geeignete Wahl der Distanzfolge lässt sich der Shellsort Algorithmus optimieren. Die 1959 mit dem Algorithmus veröffentlichte Folge $n/2k$ erreicht im schlechtesten Fall ein Verhalten von $O(n^2)$ . Die 1965 entwickelte Distanzfolge $2^k-1$ von Papernov und Stasevich erreicht beispielsweise ein asymptotischen Verhalten $O(n^{(1,5)})$ .

Im Laufe der Zeit entwickelten sich immer komplexere und bessere Distanzfolgen. Viele von Ihnen sind in ihrer Komplexität noch nicht berechnet worden, schneiden bei Tests jedoch besser ab als ihre Vorgänger. Bjorn Ponnen konnte beweisen, dass es keine Distanzfolge gibt welche besser perfomt als $O(n\:log(n)^2)$ . In der Praxis hat sich die Distanzfolge von Tokuda als effizient erwiesen.

(1) $\begin{gather*} \frac{1}{5}\left( 9 \left( \frac{9}{4} \right)^{k-1}-4 \right) \end{gather*}$

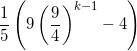
public class Shellsort {

	public static <T extends Comparable<T>>void sort(T[] source) {
		final int[] sequence = getSequence(source.length);
		for (int i = 0; i < sequence.length; i++) {
			int distance = sequence[i];
			for (int start = distance; start < source.length; start++) {
				for (int j = start; j >= distance && source[j].compareTo(source[j - distance]) <= 0; j-=distance) {
					T value = source[j];
					source[j] = source[j - distance];
					source[j - distance] = value;
				}
			}
		}
	}
	
	private static int[] getSequence(int size) {
		int[] result = new int[Double.valueOf((Math.log(size/5) / Math.log(2L))).intValue() + 1];
		result[result.length - 1] = 1;
		for (int i = result.length - 2; i >= 0; i--) {
			result[i] = (result[i+1] + 1)  * 2 - 1;
		}
		
		return result;
	}
}

Komplexität

Best	Average	Worst
O(n log(n))	O(n log(n)²)	O(n²)