LED-Streifen lösen in vielen Bereichen herkömmliche Leuchtmittel ab. Während die simpelsten von ihnen ein lediglich monotones Licht erzeugen können moderne LED-Streifen einiges Mehr. Manche Streifen besitzen über 300 LEDs und jede einzelne LED kann individuell in einer beliebigen Farbe leuchten. Was sich kompliziert anhört wurde jedoch ziemlich simpel gelöst. In diesem Artikel beschreibe ich die funktionsweise von adressierbaren LED-Streifen und das dahinterliegende Protokoll.
Adressierbare LEDs werden auch als Pixel LED bezeichnet. Der Branchenstandard wurde hier durch die WS2812B gelegt. Diese LED besitzt neben der Masse und der Spannungsversorgung einen Ein- und einen Ausgang für die Datenübertragen. Der Eingang einer LED kann kaskadierend an den Ausgang einer anderen LED gelegt werden. Innerhalb des Gehäuses befindet sich ein integrierter Schaltkreis zum verarbeiten der Daten.
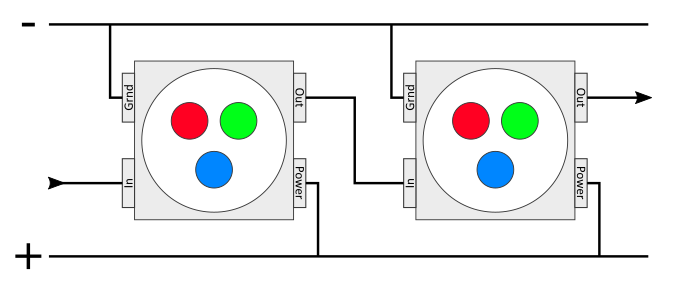
Um unterschiedliche Farben erzeugen zu können beseht die WS2821B, sowie fast jede RGB fähige LED, aus mehreren LEDs. Jede dieser LEDs kann in einer einzelnen Farbe leuchten. Genauer gesagt gibt es eine rote, eine blaue und eine grüne LED. Die Kombinationen der einzelnen Farben in unterschiedlichen Verhältnissen erzeugt eine neue Farbe. Dieses Verfahren wird als additive Farbmischung bezeichnet.
Für jede dieser drei Grundfarben sind 8 Bit-Werte vorgesehen. Insgesamt wird das RGB-Farbsignal damit in 24 Bit kodiert. Einen komplexen Algorithmus für die Signalübertragung gibt es nicht. Die Steuereinheit legt einfach der Reiche nach die Farbsingale an den Ausgang. Beginnend mit dem grünen, dem roten und dann dem kodierten Wert für das blaue Signal. Das höchste Bit wird dabei zuerst gesendet (Big-endian). Sobald die Farbsignale für die erste RGB-LED durchgelaufen sind werden die Farbsignale für die zweite LED angelegt. Dies geschieht so lange, bis für alle der adressierbaren LEDs ein Wert gesendet wurde.
Welches Signal an welche LED geschickt wird ergibt sich aus der Reihenfolge der in Reihe geschalteten LEDs. Jede LED liest dabei die ersten RGB-Werte aus der Signalfolge die sie empfängt und richtet sich danach aus. An die nächste LED wird jedoch nicht die komplette Signalfolge weiter geleitet, sondern nur der hintere Teil. Das selbst verarbeitete Signal wird von jeder einzelnen LED maskiert. Erhält die erste LED beispielsweise noch drei Farbsignale, so erhält die nächste nur noch zwei und die übernächste nur noch ein RGB-Signal.
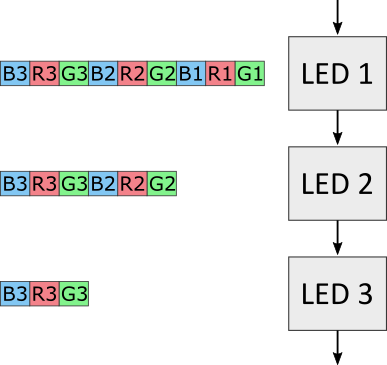
Die Aufgabe für die Steuerung ist somit ziemlich simpel: Je nach Anzahl der LEDs wird die entsprechende Anzahl an Signalen auf den Ausgang gelegt. Den einzelnen LEDs wiederum ist es dabei unwichtig an welcher Position sie sich befinden. Sie verarbeiten einfach das erste Signal das sie empfangen und leiten den Rest an ihren Ausgang weiter.
Das Prinzip ist zwar einfach, der Nachteil dieser Methode besteht jedoch darin, dass eine einzelne LED nicht direkt angesteuert werden kann. Es müssen immer alle vorgeschalteten LEDs ebenfalls mit einem Wert versorgt werden. Das bedeutet auch, dass umso länger die Kette an LEDs wird, umso langsamer können diese angesteuert werden.
Bits sind binär. Sie stehen aus 1en und 0en. Ebenso kann auf einer digitalen Leitung entweder Spannung anliegen oder nicht. Damit eine LED weiss, wann eine Signalfolge zu ende ist und wann eine neue anfängt wird ein Reset-Signal 
benötigt. Dies ist bei der WS2821B nichts weiter als eine Pause von 50 Mikrosekunden in der keine Spannung anliegt.
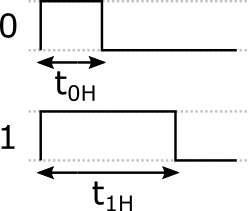
Damit ergibt sich jedoch folgende Frage: Woher weiss eine LED wann ein Reset gesendet wurde und wann eine Folge von 0-Bits? Im Protokoll der WS2821B wurde das damit gelöst, dass sowohl das 1 und das 0-Bit mit jeweils einer steigenden und einer fallenden Flanke kodiert werden. Der Abstand zwischen steigender und fallender Flanke gibt dabei Auskunft ob es sich um eine 1 oder 0 gehandelt hat.
Bei einer 0 liegt der Abstand zwischen den beiden Flanken bei 
bei 0,4 µs. Bei einer 1 
bei 0,8 µs. Einzelne Bits liegen mit einer Zeit 
von insgesamt 1,25 µs auseinander. Der Unterschied zwischen 1 und 0 liegt somit bei gerade einmal 0,4 µs. Nach dem Nyquist-Shannon-Abtasttheorem muss die Abtastrate des Schaltkreises der LED damit über 0,2 µs liegen. Damit lässt sich nun auch berechnen mit welcher Geschwindigkeit 
ein LED-Streifen mit 
LEDs aktualisiert werden kann.
(1) 
Für einen LED-Streifen mit 50 LEDs ergibt sich somit eine Aktualisierungsrate von knapp 645 Hz. Ein LED-Streifen mit 200 LEDs kann hingegen nur noch mit 175 Hz aktualisiert werden.