Insertionsort ist ein Sortierverfahren, welches einfach zu verstehen und schnell zu implementieren ist. Von anderen Sortierverfahren hebt es sich dadurch hervor, dass es sowohl stabil wie auch onlinefähig ist. Ein weiterer Vorteil besteht darin, dass der Algorithmus in-place arbeitet und somit keinen weiteren Speicherplatz benötigt. Bei all den Vorteilen, hat der Insertionsort-Algorithmus jedoch den Nachteil, dass seine Komplexität in Durchschnitt O(n²) beträgt. Damit ist er für große Datenmengen nicht mehr praktikabel einzusetzen.
Angeberwissen: Online-Algorithmus
Ein Algorithmus wird dann als Online-Fähig bezeichnet, wenn während der Sortierung oder bereits bei abgeschlossener Sortierung neue Element hinzugefügt werden können. Entscheidend dabei ist, dass die Sortierung nicht neu gestartet werden muss, sondern das bestehende Ergebnis beibehalten werden kann.
Der Insertionsort-Algorithmus iteriert der Reihe nach (links nach rechts) durch alle Elemente, beginnend vom ersten Element. In jedem Schritt wird dabei das aktuelle Element mit den vorherigen Elementen verglichen und geschaut an welcher Stelle das aktuelle Element eingefügt gehört. Alle Elemente, welche bereits verarbeitet wurden und somit hinter dem aktuellen Element liegen (linken Seite) sind bereits sortiert.
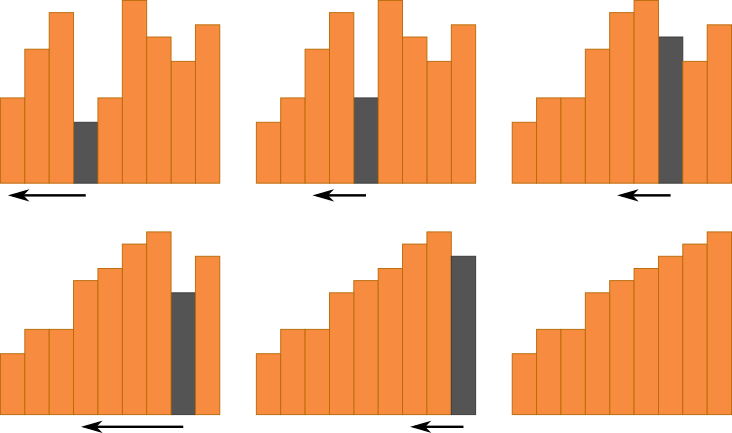
Der Insertionsort-Algorithmus lässt sich durch zwei Schleifen verwirklichen. Die erste Schleife stellt sicher, dass jedes Element betrachtet wird. Für jedes Element wird dabei eine weitere Schleife in umgekehrter Richtung durchlaufen. Es werden die bereits sortierten Elemente verglichen und diese nach Rechts verschoben, bis die Stelle erreicht wird an der das aktuelle Element richtig eingeordnet ist.
public class InsertionSort {
static <T extends Comparable<T>>void sort(T[] source) {
for (int i = 1; i < source.length; i++) {
for (int j = i; j > 0 && source[j].compareTo(source[j - 1]) <= 0; j--) {
T value = source[j];
source[j] = source[j - 1];
source[j - 1] = value;
}
}
}
}
Komplexität
| Best | Average | Worst |
| O(n) | O(n²) | O(n²) |