Die binäre Suche ist der einfachste Suchalgorithmus, welcher nicht nur stupide durch alle Element läuft. Der Algorithmus arbeitet auf einem bereits sortierten Feld(Array) und hat im besten Fall bereits mit nur einem Vergleich einen Treffer.
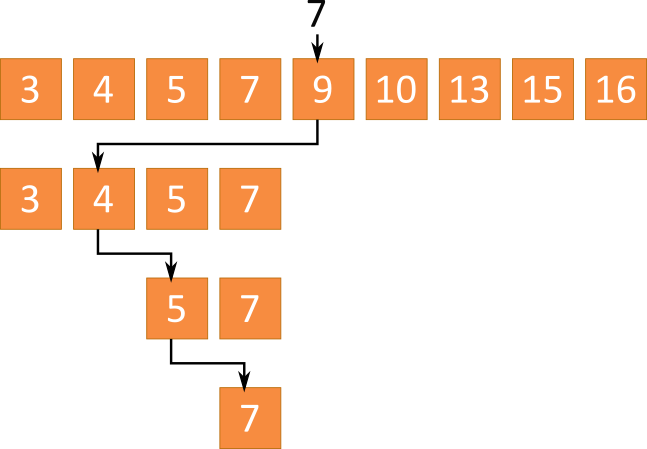
Das Array wird dabei zunächst in zwei gleich große Hälften aufgeteilt. Das Element in der Mitte wird dann mit dem zu suchenden Wert verglichen. Stimmt der Wert überein, so ist die Suche damit beendet. Trifft dies nicht zu, so wird geschaut ob der zu suchende Wert kleiner oder größer ist als das Element in der Mitte. Je nachdem wird der Suchalgorithmus dann auf der kleineren oder größeren Seite fortgesetzt. Die jeweilige Seite wird zu dem neuen Suchbereich mit dem der Algorithmus von neuem gestartet wird. Der Algorithmus lässt sich damit wunderbar in einer Schleife implementieren.
public static <T extends Comparable<T>> int binarySearch(T[] array, T item) {
int low = 0;
int high = array.length - 1;
while(low <= high) {
int mid = (high - low)/2 + low;
int compare = item.compareTo(array[mid]);
if (compare == 0) {
return mid;
}
else if (compare < 0) {
high = mid - 1;
}
else {
low = mid + 1;
}
}
return -1;
}
Komplexität
| Best | O(1) |
| Average | O(log n) |
| Worst | O(log n) |