In ein paar Jahren dürfte es soweit sein, dass die ersten Quantencomputer einsatzbereit sind. Während aktuell hauptsächlich Physiker mit der Quantentechnologie arbeiten werden dann auch erste Informatiker anfangen Algorithmen für die neue Technologie zu schreiben.
Aktuelle Programmiersprachen wie QASM sind sehr schlicht aufgebaut und erlauben nur rudimentäre Operationen. Dies ist nicht verwunderlich, da technisch noch nicht viel mehr realisiert werden kann. Die Assembler ähnelnden Sprachen dürften bald von höheren Programmiersprachen abgelöst werden. Die Grundlagen für das Rechnen mit Qauantenbits (Qubits) dürften jedoch die selben bleiben und sollten daher von jedem Informatiker der sich mit diesem Thema beschäftigt im Ansatz verstanden werden.
Die hier gezeigten Beispiele basieren auf dem Buch Quantum Computing verstehen von Matthias Homeister. Wer nicht nur damit angeben möchte sondern sich wirklich für Quantencomputer interessiert sollte sich dieses Buch als Einsteigerhilfe zulegen.
Qubit
Ein Qubit beschreibt in der Quantenmechanik die kleinste Einheit. Wie ein herkömmliches Bit kann auch ein Qubit die Zustände 1 und 0 annehmen. Dies basiert beispielsweise auf Polarisation oder dem Spin eines Teilchens. Das Qubit wird dabei in der Dirac-Notation ![]() und
und ![]() aufgeschrieben. Anders als ein herkömmliches Bit kann das Qubit beide Zustände gleichzeitig annehmen.
aufgeschrieben. Anders als ein herkömmliches Bit kann das Qubit beide Zustände gleichzeitig annehmen.
(1) ![]()
Die komplexen Zahlen ![]() und
und ![]() beschreiben die Wahrscheinlichkeit des jeweiligen Zustands und werden als Amplitude bezeichnet. Für die Amplituden gilt, dass die Summe ihrer Quadrate den Wert 1 ergeben muss.
beschreiben die Wahrscheinlichkeit des jeweiligen Zustands und werden als Amplitude bezeichnet. Für die Amplituden gilt, dass die Summe ihrer Quadrate den Wert 1 ergeben muss.
(2) ![]()
Ein Qubit in dem Zustand ![]() ist gleichermaßen im Zustand
ist gleichermaßen im Zustand ![]() und
und ![]() , da für beide Zustände
, da für beide Zustände ![]() gilt. Wird das Qubit gemessen, so wird einer dieser Zustände mit der entsprechenden Wahrscheinlichkeit angenommen. Wichtig dabei ist, dass sich das Qubit bis zu dieser Messung tatsächlich in beiden Zuständen gleichzeitig befindet. Diese Überlagerung beider Zustände wird als Superposition bezeichnet.
gilt. Wird das Qubit gemessen, so wird einer dieser Zustände mit der entsprechenden Wahrscheinlichkeit angenommen. Wichtig dabei ist, dass sich das Qubit bis zu dieser Messung tatsächlich in beiden Zuständen gleichzeitig befindet. Diese Überlagerung beider Zustände wird als Superposition bezeichnet.
Um die Arbeitsweise eines Quantencomputers zu verstehen und mit Superpositionen arbeiten zu können werden die Qubits als Basisvektoren angegeben mit der Basis {![]() ,
, ![]() }.
}.
(3) ![]()
Eine Superposition ergibt sich aus der Linearkombination der Basisvektoren.
(4) ![]()
Der Vorteil des Qubit im Vergleich zum herkömmlichen Bit liegt in seiner Superposition. Wird der Zustand des Qubits gemessen zerfällt diese Superposition und einer der Basiszustände wird angenommen. Um die Superposition zu erhalten darf das Qubit daher nicht gemessen werden. Klassische Rechenoperationen wie mit einem Bit sind mit einem Qubit daher nicht möglich. Um auf einem Qubit zu arbeiten werden quadratische 2×2-Matrizen der Form
(5) ![]()
benötigt. Mit diesen Matrizen lässt sich das Qubit transformieren ohne seinen Zustand zu messen. Durch geschickten Einsatz mehrerer Qubits und Matrizen lassen sich die Qubits so verändern, dass diese Rechenoperationen durchführen können. Die manipulation dieser Qubits geschieht in der Realität durch Mikrowellen welche auf das Qubit geschossen werden. Ohne den Zustand des Qubits zu messen kann dieser dadurch manipuliert werden. Eine mögliche Superposition bleibt dabei erhalten.
Die erwähnten Matrizen müssen unitär sein. Unitär heißt, dass eine konjungiert komplexe und transponierte Matrix ihre inverse ![]() ergibt. Mit sich selber multipliziert ergibt sich die Einheitsmatrix
ergibt. Mit sich selber multipliziert ergibt sich die Einheitsmatrix ![]() .
.
(6) ![]()
Quantengatter
Die wahrscheinlich wichtigste unitäre Matrix ist die Hadamard-Matrix ![]() . In dem Bereich des Quantencomputers werden diese 2×2-Matrizen auch Gatter genannt, da die Matrizen selbst nur mathematische Hilfsmittel darstellen. Die Hadamard-Matrix wird daher auch Hadamard-Gatter genannt.
. In dem Bereich des Quantencomputers werden diese 2×2-Matrizen auch Gatter genannt, da die Matrizen selbst nur mathematische Hilfsmittel darstellen. Die Hadamard-Matrix wird daher auch Hadamard-Gatter genannt.
(7) 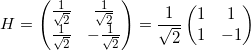
Das Hadamard-Gatter überführt ein Qubit, wie beispielsweise ![]() , in eine Superposition mit gleich großen Amplituden. Um eine Matrix auf den Vektor eines Qubit anzuwenden wird eine simple Matrix-Multiplikation durchgeführt.
, in eine Superposition mit gleich großen Amplituden. Um eine Matrix auf den Vektor eines Qubit anzuwenden wird eine simple Matrix-Multiplikation durchgeführt.
(8) 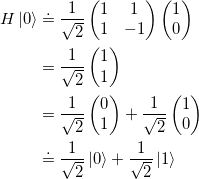
Weitere dieser Gatter sind die Pauli-Matrizen, welche sich zusammensetzen aus der Pauli-X-Transformation (Bitflip), der Pauli-Y-Transformation und der Pauli-Z-Transformation (Phaseflip), welche häufig durch Buchstaben ![]() ,
, ![]() und
und ![]() notiert werden.
notiert werden.
(9) 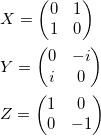
Quantenregister
Mit einem Bit alleine lässt sich nicht viel anstellen. Wie bei herkömmlichen Rechnern ist auch bei einem Quantencomputer das Zusammenspiel mehrerer Bits entscheidend. Jedes Qubit kann dabei eine Superposition einnehmen.
Das klassische Register aus ![]() Bits kann
Bits kann ![]() verschiedene Zustände annehmen. Bei einem gebräuchlichen Register von 16 Bit können damit 65.536 verschiedene Zustände angenommen werden. Das Quantenregister kann durch seine Superposition alle diese Zustände gleichzeitig annehmen. Um diese Leistung zu erzielen bräuchte ein herkömmlicher Rechner also 65.536 x 16 Bit. Das wäre ein Register in der Größe von einem Megabit. So eine Größe ist selbst in weiter Zukunft unvorstellbar. Selbst mit einem Register von 64 Bit und 4 Kernen müsste ein herkömmlicher Rechner noch immer 4096 Operationen ausführen um eine einzige Operation eines Quantencomputers zu simulieren.
verschiedene Zustände annehmen. Bei einem gebräuchlichen Register von 16 Bit können damit 65.536 verschiedene Zustände angenommen werden. Das Quantenregister kann durch seine Superposition alle diese Zustände gleichzeitig annehmen. Um diese Leistung zu erzielen bräuchte ein herkömmlicher Rechner also 65.536 x 16 Bit. Das wäre ein Register in der Größe von einem Megabit. So eine Größe ist selbst in weiter Zukunft unvorstellbar. Selbst mit einem Register von 64 Bit und 4 Kernen müsste ein herkömmlicher Rechner noch immer 4096 Operationen ausführen um eine einzige Operation eines Quantencomputers zu simulieren.
Das Einsatzgebiet dieser Operationen auf Superpositionen ist natürlich sehr beschränkt. In den meisten Fällen möchte man mit dem Ergebnis der letzten Operation weiterrechnen und interessiert sich nicht dafür, was passiert wäre, wenn die Rechnung mit einer anderen Zahl durchgeführt worden wäre. In seltenen Fällen ist die Superposition dennoch hilfreich. Bei einer verschlüsselten Datei beispielsweise könnten so alle möglichen Passwörter gleichzeitig getestet werden.
Um zwei Qubits ![]() und
und ![]() zu einem Register zusammenzufügen müssen diese Ausmultipliziert werden.
zu einem Register zusammenzufügen müssen diese Ausmultipliziert werden.
(10) ![]()
(11) ![]()
Aus vier Amplituden der Superpositionen werden paarweise multiplizierte Amplituden mit den entsprechenden Zuständen ![]() ,
, ![]() ,
, ![]() und
und ![]() . Auch für diese Amplituden gilt, dass die Summe ihrer Quadrate 1 ergeben muss.
. Auch für diese Amplituden gilt, dass die Summe ihrer Quadrate 1 ergeben muss.
(12) ![]()
Die vier neuen Zustände, welche aus den beiden Qubits resultieren können ebenfalls als Basisvektoren betrachtet werden. Dazu werden sie durch das Tensorprodukt vereint. In den hier vorgestellten Beispielen kann jedoch auf das Kronecker-Produkt zurückgegriffen werden. Dieses lässt sich bildlich sehr einfach darstellen und nachvollziehen. Einfach ausgedrückt wird das Kronecker-Produkt zweier Matrizen dadurch gebildet, dass die Elemente der ersten Matrix durch die gesamte zweite Matrix ersetzt werden. Alle inneren Elemente werden zudem mit dem Wert des Elements der ersten Matrix multipliziert.
(13) 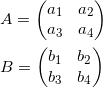
(14) 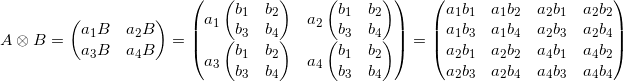
Mit dem Kronecker-Produkt lassen sich einzelne Qubits verbinden.
(15) 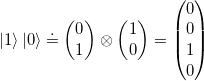
Anstelle von ![]() kann vereinfacht auch
kann vereinfacht auch ![]() geschrieben werden. Für die Basis {
geschrieben werden. Für die Basis {![]() ,
, ![]() ,
, ![]() ,
, ![]() } ergeben sich folgende Einheitsvektoren:
} ergeben sich folgende Einheitsvektoren:
(16) 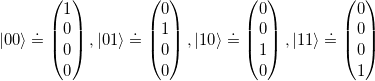
Eine Superposition des gesamten Registers kann hergestellt werden, indem jedes Qubit über die Hadamard-Matrix transformiert wird.
(17) 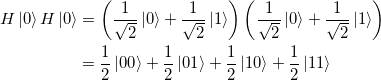
Falls eine Matrix ![]() auf dem Vektorraum
auf dem Vektorraum ![]() agiert und Matrix
agiert und Matrix ![]() auf dem Vektorraum
auf dem Vektorraum ![]() , dann gilt:
, dann gilt:
(18) ![]()
Die Formel ![]() kann somit umgestellt werden zu
kann somit umgestellt werden zu ![]() .
.
(19) 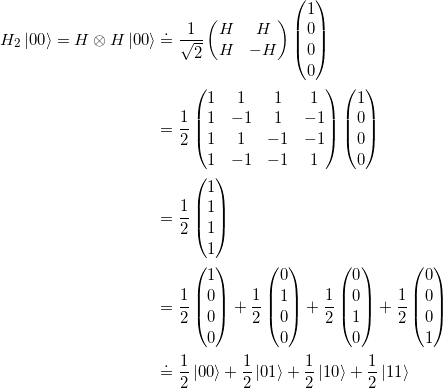
Durch die Berechnung mit Vektoren ergibt sich das gleiche Ergebnis, welches weiter oben durch Ausmultiplizieren berechnet wurde. Wichtig dabei ist, dass die jewiligen Matrizen auf dem zugehörigen Vektorraum agieren müssen. Möchten wir beispielsweise für den Zustand ![]() das erste und dritte bit mit der Hadarmard-Matrix
das erste und dritte bit mit der Hadarmard-Matrix ![]() transformieren, das zweite jedoch beibehalten, so muss die Identitätsmatrix
transformieren, das zweite jedoch beibehalten, so muss die Identitätsmatrix ![]() für das zweite Qubit angewandt werden damit die Dimensionen wieder passen. Die Transformationmatrix berechnet sich dann aus
für das zweite Qubit angewandt werden damit die Dimensionen wieder passen. Die Transformationmatrix berechnet sich dann aus ![]() .
.
Gesteuerte Quantengatter
Das simpelste Schaltnetz, dass ein Computer benötigt um rechnen zu können ist der Halbaddierer. Dieser setzt sich aus einem XOR-Gatter und einem AND-Gatter zusammen. Auch der Quantencomputer braucht diese Gatter. Sie werden realisiert durch einen zusätzlichen Eingang, mit dem es möglich ist ein inneres Gatter zu steuern.
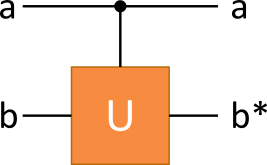
Bei dem gesteuerten Gatter wird eine Operation ![]() auf Eingang
auf Eingang ![]() ausgeführt, sofern das Qubit an Eingang
ausgeführt, sofern das Qubit an Eingang ![]() aktiv ist. Das gesteuerte Gatter lässt sich durch eine 4×4-Matrix beschreiben.
aktiv ist. Das gesteuerte Gatter lässt sich durch eine 4×4-Matrix beschreiben.
(20) 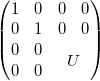
Da Quantengatter mathematisch durch unitäre Matrizen beschrieben werden, welche die Dimension des Vektors bei einer Operation beibehalten muss bei der bildlichen Darstellung des Schaltkreises darauf geachtet werden, dass die gleiche Anzahl an Ein- und Ausgängen existiert. Ein zusätzliches Bit kann in einem Schaltkreis weder erzeugt werden, noch verschwinden. Auch eine Verzweigung ist nicht möglich. Eingang ![]() wird daher unverändert auf Ausgang
wird daher unverändert auf Ausgang ![]() gelegt.
gelegt.
Wird das gesteuerte Gatter auf den Bitflip ![]() angewandt, so erhält man ein XOR-Gatter, das explizite Oder. Dieses Gatter ist als CNOT (Controlled NOT) bekannt.
angewandt, so erhält man ein XOR-Gatter, das explizite Oder. Dieses Gatter ist als CNOT (Controlled NOT) bekannt.
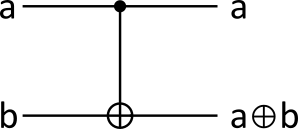
(21) 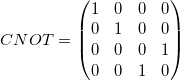
Mit dem CNOT-Gatter lassen sich durch geschicktes Hintereinanderschalten bereits alle wichtigen Operationen realisieren. Es gibt jedoch noch ein weiteres Gatter welches Operationen wie AND erheblich vereinfacht. Das Toffoli-Gatter ![]() . Um das Toffoli-Gatter zu erzeugen wird das CNOT-Gatter erneut in ein gesteuertes Gatter gepackt.
. Um das Toffoli-Gatter zu erzeugen wird das CNOT-Gatter erneut in ein gesteuertes Gatter gepackt.
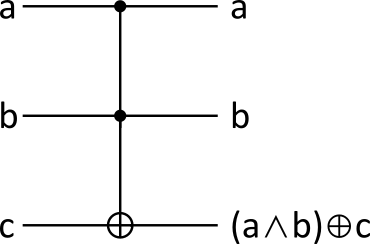
(22) 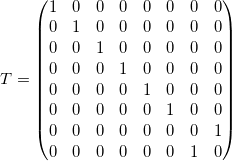
Legt man Eingang ![]() und
und ![]() auf 1, so ist der Ausgang ein negiertes
auf 1, so ist der Ausgang ein negiertes ![]() .
.
(23) ![]()
Wird der Eingang ![]() auf 0 gesetzt, so lassen sich
auf 0 gesetzt, so lassen sich ![]() und
und ![]() zu einem Und zusammenfassen.
zu einem Und zusammenfassen.
(24) ![]()
Mit dem Toffoli-Gatter ist es nun möglich auf einfache Weiße einen Halbaddierer zu konstruieren. Das Toffoli-Gatter muss dazu zu einem AND- und einem XOR-Gatter gemacht werden. Dies geschieht durch zwei Hilfsbits 1 und 0.
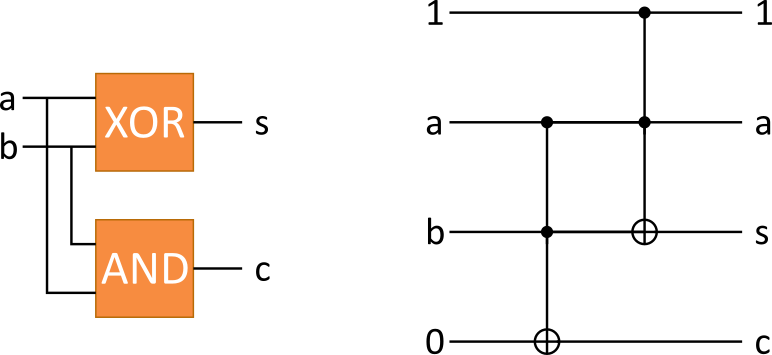
Möchten wir den dargestellten Schaltkreis mathematisch beschreiben benötigen wir für beide Operationen eine entsprechende Matrix. Das AND-Gatter bezieht sich auf das zweite, dritte und vierte Bit des Eingangsregisters ![]() und kombiniert diese mit dem ersten Toffoli-Gatter
und kombiniert diese mit dem ersten Toffoli-Gatter ![]() . Das erste Bit wird zunächst einfach nur durchgereicht. Aus diesem Grund wird auf das erste Bit die Identitätsmatrix
. Das erste Bit wird zunächst einfach nur durchgereicht. Aus diesem Grund wird auf das erste Bit die Identitätsmatrix ![]() angewandt. Die resultierende 16×16-Matrix ergibt sich aus
angewandt. Die resultierende 16×16-Matrix ergibt sich aus ![]() . Für das XOR-Gatter ist dies genau umgekehrt und das vierte Bit wird durchgereicht
. Für das XOR-Gatter ist dies genau umgekehrt und das vierte Bit wird durchgereicht ![]() . Um das Ausgangsregister
. Um das Ausgangsregister ![]() zu berechnen wird das Eingangsregister nacheinander mit beiden Matrizen multipliziert.
zu berechnen wird das Eingangsregister nacheinander mit beiden Matrizen multipliziert.
(25) ![]()
Möchte man den nun einen Addierer erstellen, der zwei 4 Bit-Werte addiert, so benötigt man ein viel größeres Register. Das erste Bit 1 kann öfter verwendet werden, da sich im Verlauf der Berechnung sein Wert nicht ändert. Das vierte Bit, die 0 die zu dem Carry-Bit ![]() wird, benötigt man jedoch auch für die anderen Additionen. Für jeden zusätzlichen Bit-Wert der addiert werden soll, werden daher 3 zusätzliche Bit benötigt. Für 4 Bit-Werte ergibt sich ein Eingangsregister von
wird, benötigt man jedoch auch für die anderen Additionen. Für jeden zusätzlichen Bit-Wert der addiert werden soll, werden daher 3 zusätzliche Bit benötigt. Für 4 Bit-Werte ergibt sich ein Eingangsregister von ![]() mit 13 Qubits. Bei den acht benötigten Matrizen handelt es sich dann jeweils um eine 8192×8192-Matrix. Würde ein normaler Rechner das simulieren müssen, so wäre das schon ein erheblicher Rechenaufwand nur um zwei 4-Bit-Werte zu addieren.
mit 13 Qubits. Bei den acht benötigten Matrizen handelt es sich dann jeweils um eine 8192×8192-Matrix. Würde ein normaler Rechner das simulieren müssen, so wäre das schon ein erheblicher Rechenaufwand nur um zwei 4-Bit-Werte zu addieren.
Auf dem Blatt Papier ist das ganze viel einfacher, da man oft durch genausen hinsehen erkennen kann, wie sich die Bits verhalten. Betrachten wir beispielsweise das Eingabe-Register ![]() für den Halbaddierer, so lässt sich leicht sagen, dass nach dem UND-Gatter das vierte Bit zu 1 wird
für den Halbaddierer, so lässt sich leicht sagen, dass nach dem UND-Gatter das vierte Bit zu 1 wird ![]() und nach dem XOR-Gatter das dritte Bit zu 0 und wir als Ergebnis
und nach dem XOR-Gatter das dritte Bit zu 0 und wir als Ergebnis ![]() erhalten. Bei Superpositionen muss diese Logik auf jeden Zustand der Superpositionen einzeln angewandt werden.
erhalten. Bei Superpositionen muss diese Logik auf jeden Zustand der Superpositionen einzeln angewandt werden.
Verschränkung
Wird ein Quantenbit gemessen, so wird die Superposition zerstört und das Messergebnis ist entweder ![]() oder
oder ![]() . Betrachtet man nicht nur ein einziges Bit sondern ein ganzes Register, welches in eine Superposition überführt wurde, so treten Eigenschaften der Quantenmechanik auf, welche weitaus schwerer zu begreifen sind als ein bloßes Teilchen, welches sich in zwei Zuständen gleichzeitig befindet. Eine dieser Eigenschaften ist die Quantenverschränkung.
. Betrachtet man nicht nur ein einziges Bit sondern ein ganzes Register, welches in eine Superposition überführt wurde, so treten Eigenschaften der Quantenmechanik auf, welche weitaus schwerer zu begreifen sind als ein bloßes Teilchen, welches sich in zwei Zuständen gleichzeitig befindet. Eine dieser Eigenschaften ist die Quantenverschränkung.
Betrachten wir hierzu den Basiszustand ![]() und wenden auf das erste Bit die Hadamard-Matrix an und auf das gesamte Register im Anschluss das CNOT-Gatter.
und wenden auf das erste Bit die Hadamard-Matrix an und auf das gesamte Register im Anschluss das CNOT-Gatter.
(26) 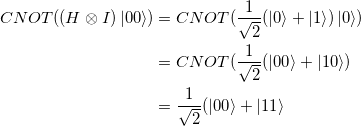
Das Quantenregister besitz nun zwei gleich wahrscheinliche Zustände ![]() und
und ![]() . Bei einer Messung können die Bits einen dieser beiden Zustände annehmen. Das interessante daran ist, dass dieser Zustand auch angenommen wird, wenn nur eines der beiden Qubits gemessen wird. Wird beispielsweise eine
. Bei einer Messung können die Bits einen dieser beiden Zustände annehmen. Das interessante daran ist, dass dieser Zustand auch angenommen wird, wenn nur eines der beiden Qubits gemessen wird. Wird beispielsweise eine ![]() für das erste Qubit gemessen, so kann davon völlig unabhängig das zweite Qubit gemessen werden und man würde auf jeden Fall
für das erste Qubit gemessen, so kann davon völlig unabhängig das zweite Qubit gemessen werden und man würde auf jeden Fall ![]() erhalten. Diese miteinander verschränkten Qubits werden als EPR-Paare bezeichnet, benannt nach den Wissenschaftlern Einstein, Podolsky und Rosen. Das Einstein-Podolsky-Rosen-Paradoxon ist eines der am häufigsten diskutierten Phänomene unter Physikern und lässt sich in einer Vielzahl von SiFi-Filmen und Büchern wieder finden.
erhalten. Diese miteinander verschränkten Qubits werden als EPR-Paare bezeichnet, benannt nach den Wissenschaftlern Einstein, Podolsky und Rosen. Das Einstein-Podolsky-Rosen-Paradoxon ist eines der am häufigsten diskutierten Phänomene unter Physikern und lässt sich in einer Vielzahl von SiFi-Filmen und Büchern wieder finden.
Die entsprechenden Zustände der verschränkten Qubits werden als Bell-Zustände bezeichnet. Es gibt vier verschiedene Bell-Zustände.
(27) 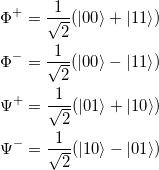
Quantenteleportation
Ein Qubit zu kopieren ist nicht möglich. Es ist möglich ein Qubit zu messen, was zur Folge hat, dass seine Superposition zerstört wird. Es gibt jedoch keine Operation ![]() die ein Qubit
die ein Qubit ![]() auf ein anderes Qubit
auf ein anderes Qubit ![]() kopieren könnte.
kopieren könnte.
(28) ![]()
Diese Eigenschaft der Qubits wird als No-Cloning-Theorem bezeichnet.
Zwar kann ein Qubit nicht kopiert werden. Es ist jedoch möglich den Zustand eines Qubits auf ein anderes Qubit zu übertragen. Der Zustand des ursprünglichen Qubits wird damit zwar zerstört, das überschriebene Qubit muss sich für diesen Vorgang jedoch nicht am selben Ort wie das ursprüngliche Qubit befinden. Dieser Vorgang wird daher auch als Quantenteleportation beschrieben.
Der Grundgedanke ist schnell erklärt: Für die Teleportation werden zwei verschränkte Qubits benötigt. Eines davon erhält Alice ![]() , das andere Bob
, das andere Bob ![]() . Alice möchte daraufhin Bob den Zustand eines weiteren Qubit
. Alice möchte daraufhin Bob den Zustand eines weiteren Qubit ![]() zukommen lassen. Sie führt dazu eine Operation auf
zukommen lassen. Sie führt dazu eine Operation auf ![]() und
und ![]() aus um herauszubekommen welche Aktion Bob ausführen muss um sein Qubit
aus um herauszubekommen welche Aktion Bob ausführen muss um sein Qubit ![]() in
in ![]() zu überführen.
zu überführen.
(29) 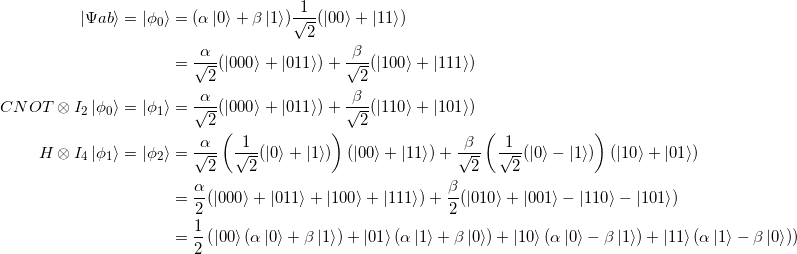
In dem hier gezeigten Beispiel hat das Qubit ![]() den Zustand
den Zustand ![]() und soll auf
und soll auf ![]() übertragen werden. Das verschränkte EPR-Paar
übertragen werden. Das verschränkte EPR-Paar ![]() befindet sich in dem Bell Zustand
befindet sich in dem Bell Zustand ![]() . Das gesamte Register aus den drei Qubit wird mit
. Das gesamte Register aus den drei Qubit wird mit ![]() abgekürzt.
abgekürzt.
In dem ersten Schritt wird auf die ersten beiden Qubits von Register ![]() Das CNOT-Gatter angewandt woraus
Das CNOT-Gatter angewandt woraus ![]() folgt. Auf das erste Qubit wird anschließend die Hadarmard-Matrix angewandt was
folgt. Auf das erste Qubit wird anschließend die Hadarmard-Matrix angewandt was ![]() zur Folge hat. Die Formel wird daraufhin so umgestellt, dass die beiden ersten Qubit des Registers ausgeklammert stehen. Dadurch ist es einfacher zu erkennen, welchen Zustand das dritte Qubit annimmt, sobald die Messung der ersten beiden Bits erfolgt. Während der oben gezeigten Transformationen wurde das dritte Bit
zur Folge hat. Die Formel wird daraufhin so umgestellt, dass die beiden ersten Qubit des Registers ausgeklammert stehen. Dadurch ist es einfacher zu erkennen, welchen Zustand das dritte Qubit annimmt, sobald die Messung der ersten beiden Bits erfolgt. Während der oben gezeigten Transformationen wurde das dritte Bit ![]() nicht angetastet. Es kann daher angenommen werden, dass sich dieses Qubit an einem anderen Ort als die anderen beiden befindet.
nicht angetastet. Es kann daher angenommen werden, dass sich dieses Qubit an einem anderen Ort als die anderen beiden befindet.
In unserem Beispiel würde Alice nun die beiden ersten Qubits von ![]() messen und kann damit auf den Zustand von Bobs Qubit schließen.
messen und kann damit auf den Zustand von Bobs Qubit schließen.
| Alice | Bob |
Alice teilt Bob nun nicht mit, in welchen Zustand sein Qubit ist, sondern sagt Bob nur was er machen muss, damit er sein Qubit in den Zustand ![]() versetzten kann. Misst Alice beispielsweise
versetzten kann. Misst Alice beispielsweise ![]() so befindet sich Bobs Qubit bereits in dem gewünschten Zustand und er könnte mit diesem arbeiten. Misst Alice hingegen
so befindet sich Bobs Qubit bereits in dem gewünschten Zustand und er könnte mit diesem arbeiten. Misst Alice hingegen ![]() so sagt sie zu Bob, dass er auf sein Qubit das Bitflip-Gatter
so sagt sie zu Bob, dass er auf sein Qubit das Bitflip-Gatter ![]() anwenden muss um
anwenden muss um ![]() zu erhalten. Bei
zu erhalten. Bei ![]() führt Bob einen Phaseflip
führt Bob einen Phaseflip ![]() aus und bei
aus und bei ![]() beide Operationen hintereinander.
beide Operationen hintereinander.
Würde eine dritte Person Alice und Bob dabei belauschen, welche Operationen Bob ausführen muss, so würde er dadurch keine brauchbare Information erhalten. Ohne das anfängliche Qubit ![]() , welches sich in Bobs Besitzt befindet, kann auch nicht auf das geheime Ergebnis
, welches sich in Bobs Besitzt befindet, kann auch nicht auf das geheime Ergebnis ![]() der Transformation geschlossen werden.
der Transformation geschlossen werden.
Die Quantenteleportation kann nicht schneller als Lichtgeschwindigkeit stattfinden. Zwar ist das EPR-Paar verschränkt und nimmt bei einer Messung einen auf beiden Seiten gekoppelten Zustand ein, Alice benötigt jedoch immer noch einen weiteren Informationskanal um Bob mitzuteilen welche Operationen er auf seinem Qubit ausführen muss um die gewünschte Information zu übertragen.
Quantenalgorithmen
Die folgenden Algorithmen beschreiben die aktuellen Einsatzmöglichkeiten von Quantencomputern. Eine genaue Beschreibung und Herleitung der einzelnen Algorithmen findet sich in dem bereits erwähnten Buch von Matthias Homeister.
- Mit dem Deutsch-Jozsa-Algorithmus lässt sich ermitteln ob eine Funktion
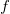 balanciert
balanciert 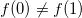 oder konstant
oder konstant 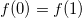 ist. Die Fragestellung wird als Problem von Deutsch bezeichnet und lässt sich durch Quantencomputer mit nur einem Zugriff auf die Funktion auswerten.
ist. Die Fragestellung wird als Problem von Deutsch bezeichnet und lässt sich durch Quantencomputer mit nur einem Zugriff auf die Funktion auswerten. - Durch den Shor-Algorithmus lässt sich eine Zahl in polynomischer Zeit
faktorisieren. Dies ist vor allen Dingen bei kryptographischen Verfahren bedeutsam, da diese auf der nicht trivialen Berechnung von Primzahlen beruhen. - Bestandteil des Shor-Algorithmus ist die Quanten-Fouriertransformation, welche es erlaubt eine Funktion in ihre Frequenzen zu zerlegen.
- Das BB84-Protokoll beschreibt ein Verfahren zum sicheren Austausch von privaten Schlüsseln um eine sichere Kommunikation zu ermöglichen. Wie der Name vermuten lässt wurde das Protokoll bereits 1984 entwickelt.
- Der Grover-Algorithmus erlaubt es eine Suche in einer unsortierten Datenbank mit
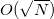 Schritten durchzuführen. Da sich viele Probleme in der Informatik auf Suchen herunterbrechen lassen bieten Quantencomputer hier einen erheblichen Vorteil gegenüber anderen Suchverfahren.
Schritten durchzuführen. Da sich viele Probleme in der Informatik auf Suchen herunterbrechen lassen bieten Quantencomputer hier einen erheblichen Vorteil gegenüber anderen Suchverfahren.